Če izvajate trdnostne simulacije s programi za analizo s končnimi elementi, ste se že zelo verjetno srečali z izrazoma “linearna” in “nelinearna” analiza. Ampak ali veste kdaj je potrebno uporabiti nelinearen pristop? V inženirskem svetu ne obstaja niti en dejansko linearen sistem, lahko pa včasih uporabimo aproksimacije, ki so “dovolj” dobre za našo aplikacijo. Kako izbrati pravilni pristop in prepoznati prednosti in slabosti obeh ter kako vam pri tem pomaga 3DEXPERIENCE® platforma, si lahko preberete v tem blogu.
Kdaj je nelinearno odzivanje materiala pomembno?
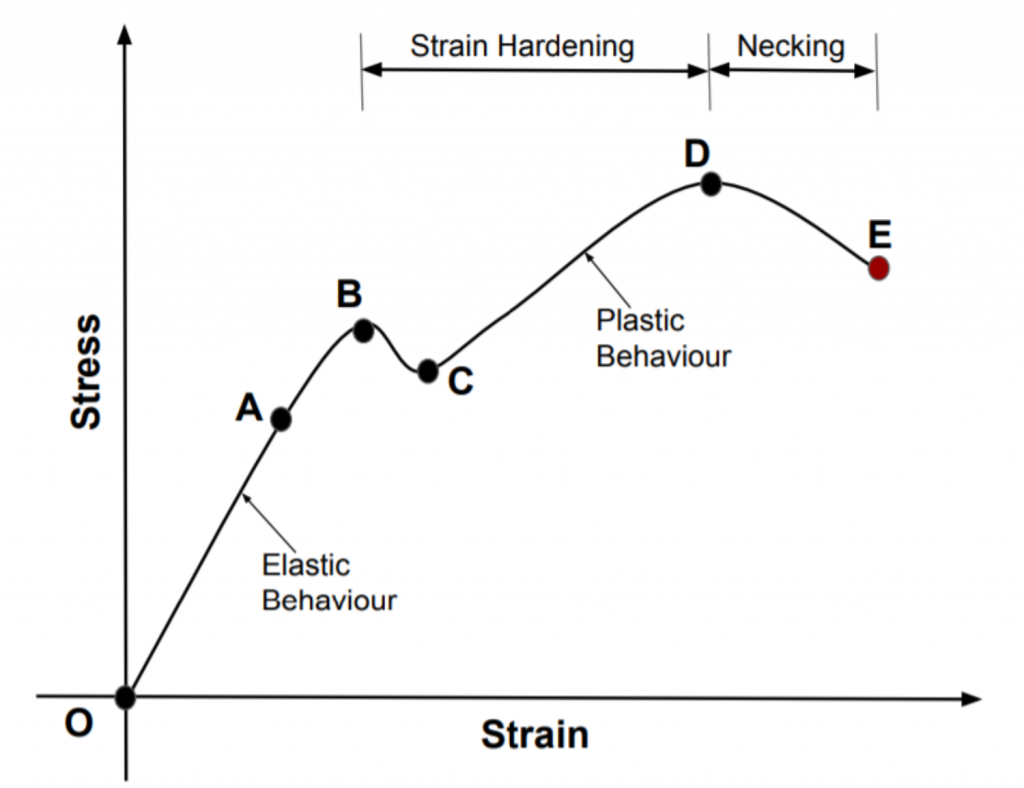
Preden se vprašamo kdaj je smiselno uporabiti nelinearni model, je potrebno razumeti katere veličine so med seboj nelinearno odvisne. Pri analizah s končnimi elementi so najprej izračunani pomiki konstrukcije, na podlagi njih in predpisanih robnih pogojev pa so izračunane deformacije. Če sledimo Hookovem reološkemu zakonu, ki popisuje odvisnost med napetostmi in deformacijami preko sorazmernostnega faktorja imenovanega modul elastičnosti, dobimo linearno odzivnost napetosti v materialu glede na podane obremenitve. Zavedati pa se je potrebno, da se vsi materiali odzivajo nelinearno, le da inženirji aproksimiramo del tega odziva kot linearno odvisnost med napetostmi in deformacijami zaradi poenostavitve in lažjega preračuna. Ta aproksimacija “majhnih pomikov” vključuje 2 zelo pomembni predpostavki:
- da deformacija ne vpliva na togost naše konstrukcije in
- da stabilnost ne predstavlja problema.
Kot primer si lahko pogledamo kovine, ki se po večini obnašajo elastoplastično. Jeklo ima značilno mejo plastičnosti – območje, v katerem se material odziva plastično in se po obremenjevanju ne povrne v prvotno stanje. Do te meje se obnaša elastično, z drugimi besedami pri obremenjevanju shranjuje energijo kot elastično potencialno energijo, ki jo v inženirski praksi imenujemo deformacijska enegija. Idealno elastičen material se v tem območju po obremenjevanju povrne v prvotno stanje, kar si lahko predstavljamo z delovanjem vzmeti. Ker pa noben material ni idealno elastičen, se je potrebno odločiti pri kateri vrednosti deformacije še smatramo material kot linearno elastičen. Najpogosteje uporabljena meja plastičnosti znaša 0.2 % deformacije po obremenitvi. To pomeni, da se material po obremenjevanju vrne do 99.8 % prvotnega stanja, v katerem je bil pred obremenjevanjem. Če uporabljamo material, ki bo pri obratovanju podvržen napetostim, ki bodo pod mejo elastičnosti, lahko v simulacijah in preračunih privzamemo linearno obnašanje – od tukaj izvira tudi predpostavka majhnih deformacij. Ko je meja elastičnosti presežena, preide material v območje plastičnosti – območje nelinearnosti in trajnih deformacij. Kadar želimo analizirati velike deformacije materiala, hitre procese kot so padci in trki, se ne moremo izogniti nelinearnim simulacijam.

Vsak material pa ima svojo značilno obliko krivulje napetosti-deformacije. Na zgornji sliki sta prikazana primera za dva različna materiala. Rdeča krivulja prikazuje odzivanje krhkega materiala, na primer stekla, keramike in nekaterih specifičnih zlitin. Absorbirana energija je majhna, prav tako pa so tudi deformacije majhne vse do porušitve materiala, ki se zgodi nenadno. Material se poruši z značilnim krhkim lomom. Za razliko od krhkih imajo duktilni materiali večjo sposobnost absorbcije energije, pri čemer imajo ponavadi nižjo mejo plastičnosti, kar lahko vpliva na našo odločitev o linearni aproksimaciji.
Kot zanimivost: Temperatura materiala izrazito vpliva na obliko krivulje napetosti-deformacije. Jekla, ki so v splošnem relativno duktilna, lahko pri nizkih temperaturah preidejo v krhko stanje. Jeklene kovice, ki so spajale plošče trupa Titanika, so imele zaradi nedovršenih procesov proizvodnje jekla majhno vsebnost mangana in veliko koncentracijo žvepla. Kombinacija vsebnosti teh dveh legirnih elementov je v temperaturnem območju Atlantskega oceana, katerega temperatura je takrat znašala približno 2 °C, povzročila tranzicijo jekla iz duktilnega v krho stanje, kar je bil eden izmed glavnih razlogov za porušitev jeklenega trupa in potopitev ladje Titanik.
Tako na nelinearnost modelov vpliva ogromno faktorjev, na katere morajo inženirji pomisliti pri izvajanju simulacij.
Vrste nelinearnosti
V našem modelu se lahko pojavi ena izmed 3 nelinearnosti ali kombinacijah le teh:
- Geometrijska
- Materialna
- Nelinearnost robnih pogojev
V tem blogu se bomo osredotočili na materialno nelinearnost. Prednosti uporabe nelinearnih modelov so med drugimi:
- Realno obnašanje materiala
- Edini način za analizo posebnih materialov, ki so hiperelastični
- Obremenjevanje z visoko hitrostjo in dinamika
Točnost izračunov pa po drugi strani s seboj prinese nekaj slabosti:
- Povečan čas za preračun
- Povečano kompleksnost
- Možnost nestabilnosti preračuna
Kot smo povedali v prejšnjem poglavju se različni materiali različno odzivajo na obremenitve. Polimeri se odzivajo linearno z izrazito mejo plastičnosti. Za to mejo se rahlo zmehčajo, pri čemer sledi velika deformacija, pred porušitvijo pa je opazno tudi deformacijsko utrjevanje materiala. Na spodnji sliki lahko vidimo, da se hiperelastični materiali tudi pri majhnih pomikih ne obnašajo linearno, zato jih moramo vedno modelirati z nelinearnim pristopom.
Posebne oblike materialne nelinearnosti imajo tudi zlitine s spominskimi lastnostmi. Spodnja slika prikazuje tudi histerezni učinek, ki je velikokrat povezan s temperaturo in hitrostjo obremenjevanja. Pri gumah lahko velikokrat opazimo mehansko histerezo, ki vpliva na različen potek obremenjevanja in sproščanja materiala.

Polimeri so podvrženi tudi lezenju, ki predstavlja časovno odvisno deformacijo. Material, ki je obremenjen z napetostjo nižjo od meje elastičnosti, se bo pri konstantnem obremenjevanju in povišani temperaturi v dolgem časovnem obdobju trajno deformiral, pri čemer se deformacija s časom povečuje.
Kot vidimo obstaja ogromno aplikacij, kjer je uporaba nelinearnih modelov neizogibna. Kako pa nam pri tem pomaga 3DExperience platforma?
Materialni modeli na 3DEXPERIENCE platformi
3DExperience platforma pokriva veliko večino materialnih modelov. Ponuja široko paleto možnosti analize plastifikacije kovin, hiperelastičnih materialov in drugih posebnih materialnih odzivov. Omogoča tudi definiranje lastnih materialnih modelov, ki najbolje popisujejo vašo specifično aplikacijo, vendar je vedno manj potrebe po tem, saj se Abaqus knjižnica teh modelov stalno dovršuje. Izbirate lahko celo med modeli za viskoelastičnost in lezenje ter materiali ojačanimi z ogljikovimi vlakni.

V primerjavi s SOLIDWORKS Simulation, 3DEXPERIENCE platforma omogoča izjemno hitro preračunavanje nelinearnih sistemov enačb, ki se v splošnem računajo z inkrementalnim pristopom, ki zahteva veliko daljše čase računanja kot pri linearnih sistemih, hkrati pa so lahko nelinearni modeli iz vidika zagotavljanja ravnovesja nestabilni.
Aplikacija za kalibriranje materialov
Kadar imamo možnost testirati uporabljen material, dobimo pri nateznem preizkusu množico točk, ki popisujejo napetosti in deformacije materiala med obremenjevanjem.
Te podatke je možno uvoziti na 3DEXPERIENCE platformo. Pri uvozu imamo možnost izbrati, če se podatki nanašajo na dejanske ali na inženirske napetosti. Nato lahko izbiramo med obstoječimi materialnimi modeli in prilegamo krivuljo našim podatkom, ki je nato avtomatsko kalibrirana tako, da popisuje lastnosti našega materiala. Na voljo imamo tudi indikatorje stabilnosti, ki nam pokažejo pri katerih vrednostih normirane deformacije postane model nestabilen.

Če povzamemo, lahko Hookov zakon uporabite ob predpostavki, da je material linearno elastičen, izotropen in homogen. Potrebno se je zavedati, da se s takšnim materialom redkokdaj srečamo v vsakdanjem življenju. Pri nelinearni simulaciji se tekom reševanja sproti preračunava in posodoblja globalna togostna matrika, ki nam omogoča obravnavo spreminjajoče togosti materiala med obratovanjem in podaja točne in zaupanja vredne rezultate za našo analizo.