UVOD
Na risbi predpisane mere kosa smejo po izdelavi le minimalno odstopati od predpisane imenske mere. Dejanska izmera je vedno večja ali manjša od predpisane mere na risbi. Za omejitev odstopanja je nujno potrebno določiti dve mejni meri, med katerima sme ležati dejanska mera. Mero z zgornjim odstopkom imenjujemo največjo ali zgornjo, s spodnjim odstopkom pa najmanjšo ali spodnjo mejno mero. Razliko med mejnima merama imenujemo tolerančna mera T ali pogosto samo toleranca, površino med zgornjo in spodnjo mero pa tolerančno polje.
OSNOVNI POJMI GLEDE TOLERANC
Imenska mera je mera, od katere sta izpeljani mejni meri, določeni z zgornjim in spodnjim odstopkom mere. Imenska mera je lahko celo ali decimalno število.
Ničelnica je pri grafični ponazoritvi mejnih mer in ujemov črta, ki pomeni imensko mero, na katero se nanašajo odstopki mere in toleranca.
Mejni meri sta dopustni meri oblikovanega elementa, med katerima mora biti dejanska mera izdelanega modela.
Največja mera je največja dopustna mera oblikovnega modela.
Najmanjša mera je najmanjša dopustna mera oblikovnega modela.
Sistem mejnih mer je sistem priporočenih (standardiziranih) toleranc in odstopkov mere.
Dejanska mera je mera, ki jo ugotovimo z merjenjem.
Odstopka izmerimo vedno od ničelnice, ki jo določimo z imensko mero.
Zgornji odstopek mere je algebrajska razlika med največjo mero in imensko mero, spodnji odstopek mere pa algebrajska razlika med najmanjšo mero in imensko mero. Iz tega sledi, da imata odstopka različna predznaka (+ ali -) in ponazarjata lego tolerančnega polja glede na ničelnico.
Toleranca mere je razlika med največjo in najmanjšo mero, torej tudi razlika med zgornjim in spodnjim odstopkom mere. Toleranca je absolutna vrednost, in zato brez predznaka.
Velikost tolerance je odvisna od imenske mere in višine tolerančnega polja, prilagaja se glede na namen uporabe predmeta. Toleranca naj bo izbrana primerno, tako da zaradi pretirane in nepotrebne natančnosti izdelave kosa ne podražimo.
OSNOVNI POJMI GLEDE UJEMOV
Posamezni elementi morajo biti tako izdelani in dokončani, da jih lahko poljubno menjamo in sestavljamo. Namen uporabe mora biti dosežen brez dodatne ali naknadne obdelave. Sestavljena elementa sta zaradi različnih največjih in najmanjših mer v ustreznem ujemu. Pogost primer ujema je družitev izvrtine in čepa.
Ujem je skladnost, dobljena iz razlike med merama dveh združenih oblikovnih elementov. Dva, ujemu pripadajoča dela imata enako imensko mero.
Naležni elementi so predmeti z eno ali več naležnimi površinami. Naležne površine so določene z mero na notranji ali zunanji površini. Izvrtine in gredi imajo cilindrične naležne površine in so v krožnem ujemu. Ujem med dvema vzporednima ravninama pa imenujemo ravni ujem. Pripadajoče naležne ravnine imajo glede na medsebojno lego pozitivni ali negativni ohlap.
Ohlap (pozitivni ohlap). Notranja mera na zunanjem delu (mera notranje naležne površine) je večja od zunanje mere na notranjem delu (mera zunanje naležne površine) in je pozitivna razlika med mero luknje in mero gredi pred sestavljanjem, če je premer gredi manjši od premera luknje.
Največji ohlap (največji pozitivni ohlap) je razlika med največjo mero zunanjega dela in najmanjšo mero notranjega dela.
Najmanjši ohlap (najmanjši pozitivni ohlap) je razlika med najmanjšo mero zunanjega dela in največjo mero notranjega dela.
Nadmera (negativni ohlap). Notranja mera zunanjega dela (mera notranje naležne površine) je manjša od zunanje mere notranjega dela (mera zunanje naležne površine) in je negativna razlika med mero luknje in mero gredi pred druženjem, če je premer gredi večji od premera luknje.
Največja nadmera (največji negativni ohlap) je razlika med najmanjšo mero notranjega dela in največjo mero zunanjega dela.
Najmanjša nadmera (najmanjši negativni ohlap) je razlika med največjo mero notranjega dela in najmanjšo mero zunanjega dela.
Ujemna toleranca je aritmetična vsota toleranc obeh oblikovnih elementov, ki spadata k ujemu. Ujemna toleranca je absolutna vrednost, zato je brez predznaka.
IZRAČUN TOLERANC IN UJEMOV BREZ POMOČI TABEL
Kot omenjeno sta osnovna elementa po tolerančnem sistemu ISO premer luknje D (notranja mera) ter premer čepa d (zunanja mera):
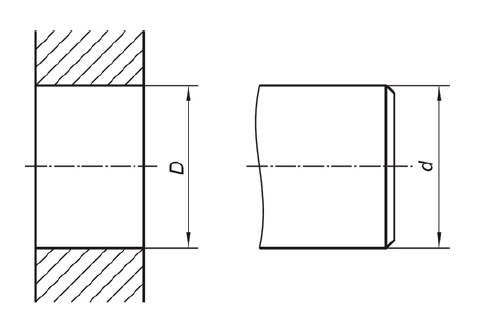
Veličine za opis toleranc dolžinskih mer po tolerančnem sistemu ISO pa so dopustna odstopanja dejanske mere (slika a)) ter dopustni odstopki mere (slika b)). Vsi elemti so ponazorjeni na spodnjih dveh slikah.
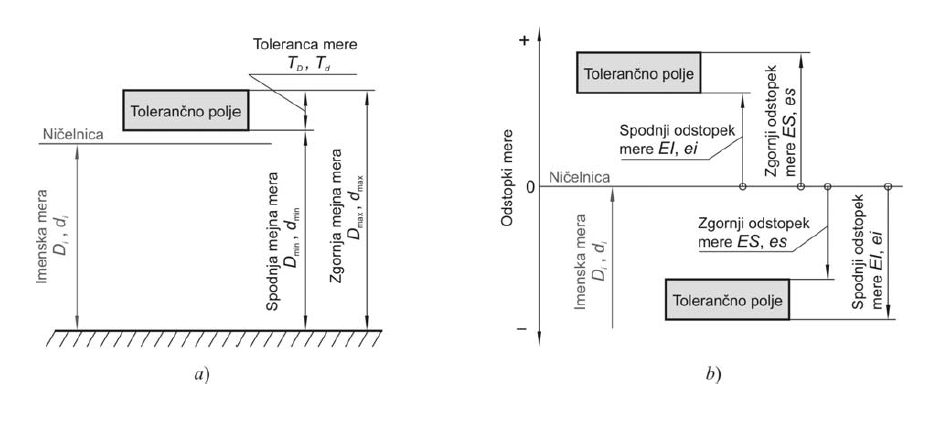
Če še enkrat ponovimo relevantne pojme za izračun toleranc brez pomoči tabel; ničelnica je pri grafični ponazoritvi mejnih mer in odstopkov ravna črta, ki predstavlja imensko mero.
Imenska mera je teoretična (želena) mera, na osnovi katere sta izpeljani obe mejni meri. Imenska mera je lahko celo ali decimalno število. Tu bo imensko mero označili kot Di za luknjo ter kot di za čep.
Zgornja mejna mera je največja dopustna mera, ki jo lahko ima luknja oziroma čep. Tu bomo za luknjo uporabili oznako Dmax ter za čep oznako dmax.
Zgornjo mejno mero za luknjo in za čep izračunamo po sledečih enačbah: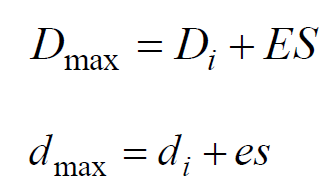 kjer je
kjer je
Dmax – zgornja mejna mera za luknjo
Di – imenska mera za luknjo
ES – zgornji odstopek za luknjo
dmax – zgornja mejna meja za čep
di – imenska mera za čep
es – zgornji odstopek za čep
Spodnja mejna mera je najmanjša dopustna mera, ki jo lahko ima luknja (Dmin) oziroma čep (dmin).
Spodnjo mejno mero za luknjo in za čep izračunamo po sledečih enačbah:
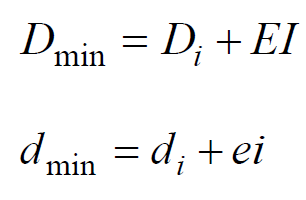
kjer je
Dmin – najmanjša dopustna mera, ki jo lahko ima luknja
Di – imenska mera za luknjo
EI – spodnji odstopek za luknjo
dmin – najmanjša dopustna mera, ki jo lahko ima čep
di – imenska mera za čep
ei – spodnji odstopek za čep
Zgornji odstopek mere pa se izračuna po sledeči enačbi (ES za luknjo, es za čep):
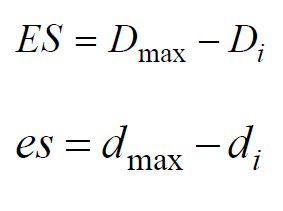
kjer je
Dmax – zgornja mejna mera za luknjo
Di – imenska mera za luknjo
dmax – zgornja mejna mera za čep
di – imenska mera za čep
Toleranca mere (TD za lukno ter Td za čep) predstavlja velikost tolerančnega polja. Kot omenjeno, je velikost tolerančnega polja algebrajska razlika med zgornjo in spodnjo mejno mero oz. zgornjim in spodnjim odstopkom mere. Izračunajo se po sledečih enačbah:
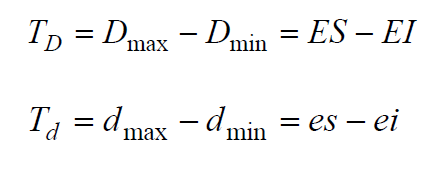
Vse elemente, ki nastopajo v enačbi smo že omenili.
Možno je izračunati tudi velikost tolerančnih polj. Velikost ISO tolerance je odvisna od velikosti imenske mere. Zato so po ISO sistemu mere od 1 do 500 mm radeljene na 13, mere od 500 do 3150 mm pa na 8 številčnih področij.
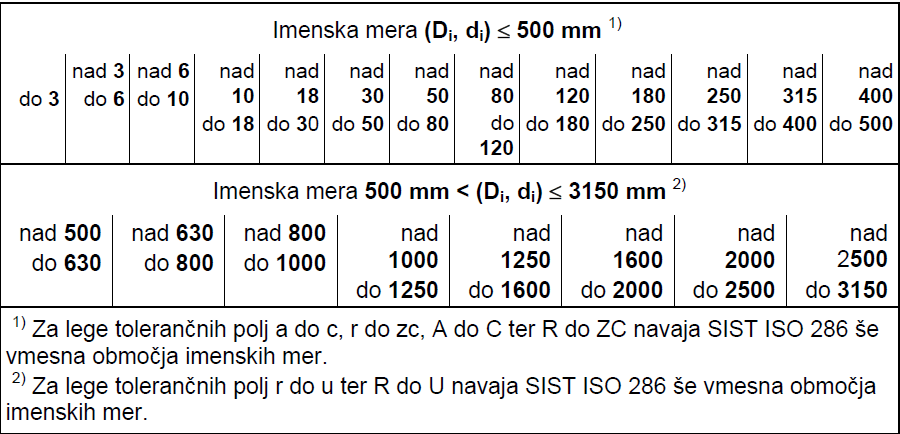
Poleg velikosti same imenske mere vpliva na velikost ISO tolerance tudi točnost izdelave, ki je neposredno vezana na kvaliteto obdelovalnega postopka. Zato je bila uvedena ISO tolerančna vrsta, ki jo sestavlja 20 osnovnih tolerančnih stopenj (IT00, IT01, IT1 IT 2 do IT18) – kvalitet izdelave. Majhna številka pomeni majhno toleranco in zelo veliko natančnost pri izdelavi. Pri kvaliteti izdelave od IT5 navzgor je osnovna velikost tolerančnega polja mnogokratnik tolerančnega koeficienta.
Tolerančni koeficient (enota) popiše velikost tolerančnega polja v mikrometrih. Izračunamo ga po sledečih enačbah:
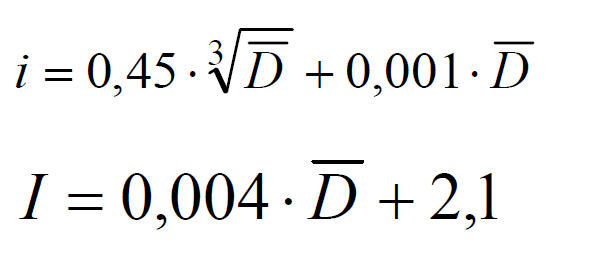
kjer je
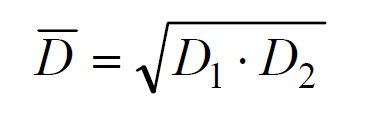
Vrednost D je geometrična srednja vrednost najmanjše in največje mere ustreznega številčnega področja, izražena v mm.
PREVERJANJE TOČNOSTI TOLERANC V PRAKSI
Ko merimo tolerance oz. mere v praksi, lahko merimo le dejanske mere. Za to se uporabljajo standardna orodja, kot so kljunasta merila, mikrometri, kladice/urice in celo CMM stroji.
Površina obdelanih teles bo zaradi obdelave bolj ali manj razbrazdana. Na različnih velikostih opazovanja se to kaže kot odstopek dimenzije, valovitost in hrapavost. Vzroke, zakaj ne moremo izdelati idealno natančne površne, lahko razdelimo v tri skupine:
- ODSTOPKI ZARADI OBDELOVANCA
- nehomogenost materiala
- deformacija obdelovancev
- krajevno različna porazdelitev temeperatur pri procesu obdelave
- pojav notranjih napetosti po obdelovalnem procesu
- sprememba trdote pri toplotni obdelavi
2. ODSTOPKI ZARADI OBDELAVE
- statični in/ali dinamični odstopki oblike in položaja vodil gibajočih se strojnih komponent
- pozicionirni odstipki gibajočih se komponent zaradi nenatančnosti merilnih in krmilnih sistemov
- elastične spremembe oblike strojev, vodil ali orodij zaradi lastne teže obdelovanca in/ali zaradi obdelovalne sile
- obraba orodij, orodnih držal in vpenjal
- nihanja v sistemu obdelovanec-orodje-stroj
- nepravilno vpetje obdelovanca v stroj
3. ODSTOPKI ZARADI OKOLICE
- krajevna in/ali časovna temperaturna nihanja, ki vplivajo na deformacijo strojev in vodil in obdelovanca (dimenzije in fizične lastnosti)
- nihanja, ki se na stroj prenašajo s tal preko temeljev, vlaga
Iz izkušenj vemo, da je vsaj polovica tolerančnega prostora izrabljenega z odstopki oblike, tako da za odstopke pozicije ostane le malo prostora. Zato je nujno podvzeti ukrepe za zmanjšanje teh odstopkov. Odstopke lahko razdelimo v šest različnih redov:
- Odstopki geometrije izdelka prvega reda (odstopek oblike): sem spadajo predvsem odstopki ravnosti in okroglosti
- Odstopki geometrije drugega reda (valovitost): se kažejo kot valovi na površini izdelka
- Odstopki geometrije tretjega, četrtega in petega reda (hrapavost): se kaže v obliki raz, zarez, lusk, izbočin ter neprimerne mikrostrukture materiala
- Odstopki geometrije šestega reda: se kaže v neprimerni mikrostrukturi materiala
Spodaj je naštetih nekaj toleranc oblike in kako jih merimo.
RAVNOST
Ravnost je lastnost površine, da vse točke na površini ležijo v eni ravnini (slika 1):
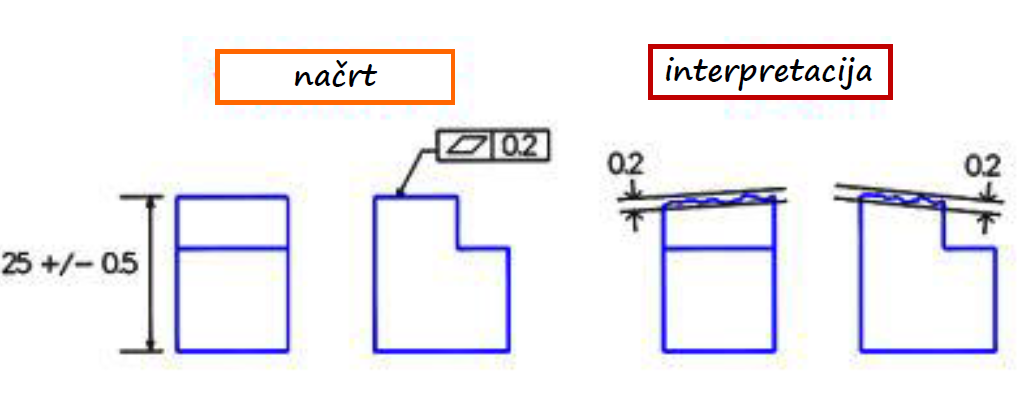
Slika 1: Obdelana površina mora ležati znotraj vzporednih ravnin, ki sta 0.25 mm narazen. Poleg tega mora biti znotraj tolerance za višino izdelka.
MERJENJE RAVNOSTI
Za merjenje ravnosti v praksi uporabljamo orodja kot so ravnila, kladice in/ali urice, merilne daljnoglede, laserje, avtokolimatorje ter CMM stroje.
Na sliki 2 je viden primer merjenja z avtokolimatorjem medtem ko je na sliki 3 viden primer tipalnega merjenja z rotacijo (CMM stroj). Na sliki 4 je viden primer merjenja ravnosti na primeru kovinskih plošč.
Slika 2: Primer merjenja z avtokolimatorjem.
Slika 3: Primer tipalnega merjenja z rotacijo.
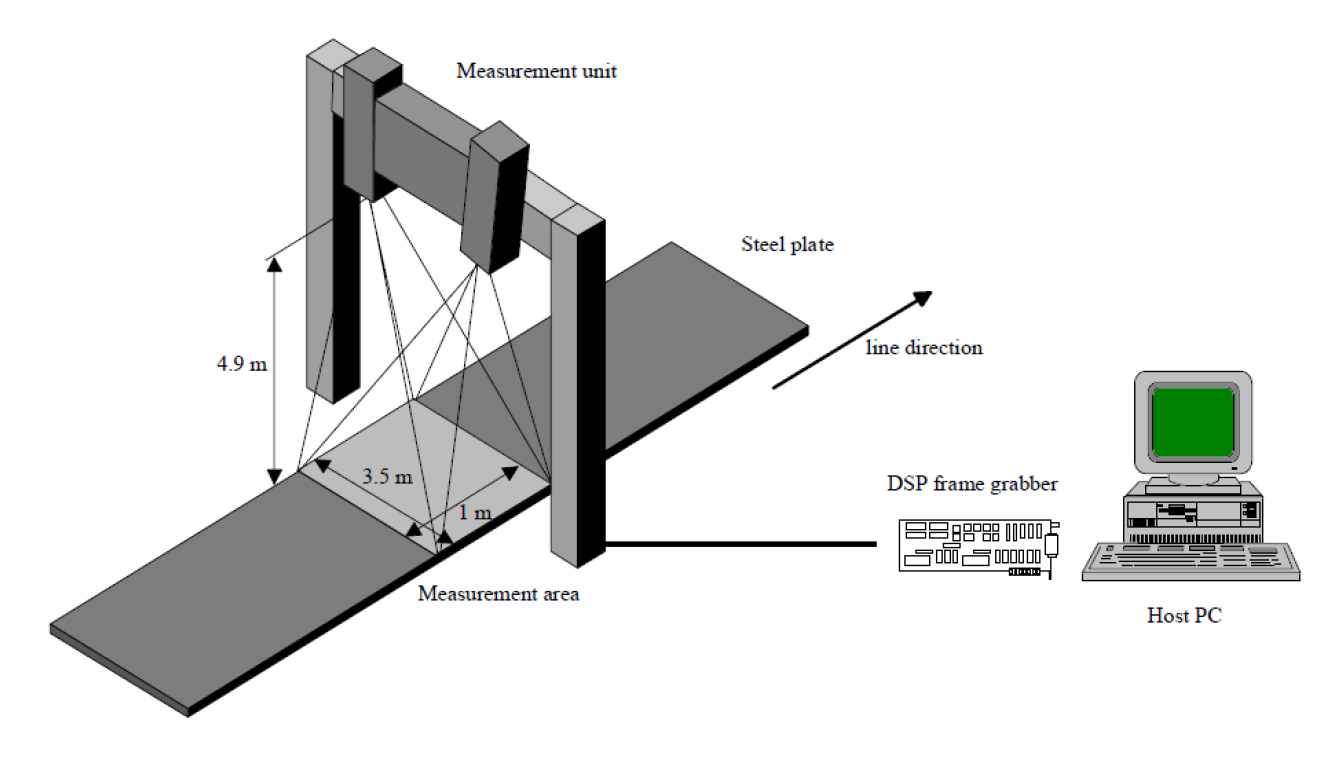
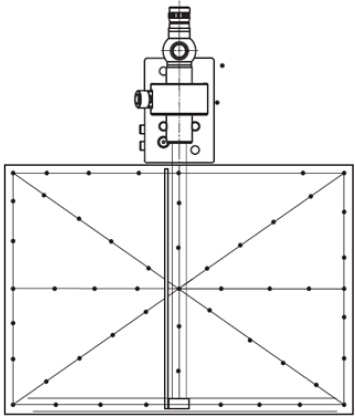
Slika 4: Primer merjenja ravnosti kovinskih plošč.
KROŽNOST
Toleranco krožnosti rabimo zato, da kontroliramo okroglost okroglih delov, kot so npr. gredi, krogle in stožci. Okrogle površine so velikokrat uporabljene v sklopih gibajočih delov, kot so ležaji ali osi. Dobra okroglost teh delov omogoča, da se ti deli gladko gibljejo in se enakomerno obrabljajo. Ker se toleranca krožnosti nanaša na eno samo površino, ne potrebujemo reference.
MERJENJE KROŽNOSTI
Pri merjencih, ki imajo na obeh koncih centrirne izvrtine je toleranco krožnosti mogoče zelo preprosto preverjati tako, da merjenec vpnemo med konici. Uporabimo lahko sinusni merilnik ali še preprostejše vpenjalo (slika 5).
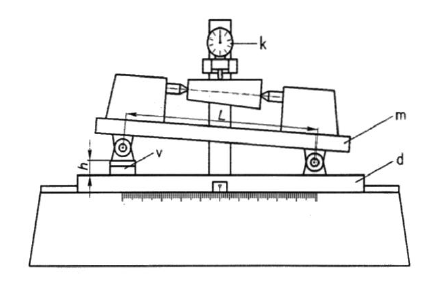
Slika 5: Primer preprostega vpenjala za merjenje krožnosti.
Slika 6 nam prikazuje dvotočkovno in tritočkovno preverjanje okroglosti, medtem ko je na sliki 7 prikazan merilnik z vrtečim merjencem in tipalom, ki obkroža merjenec.
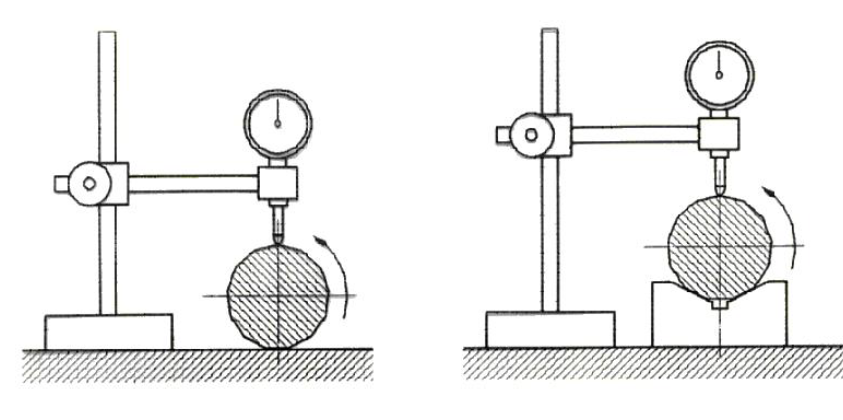
Slika 6: Primer dvotočkovnega in tritočkovnega preverjanja okroglosti.
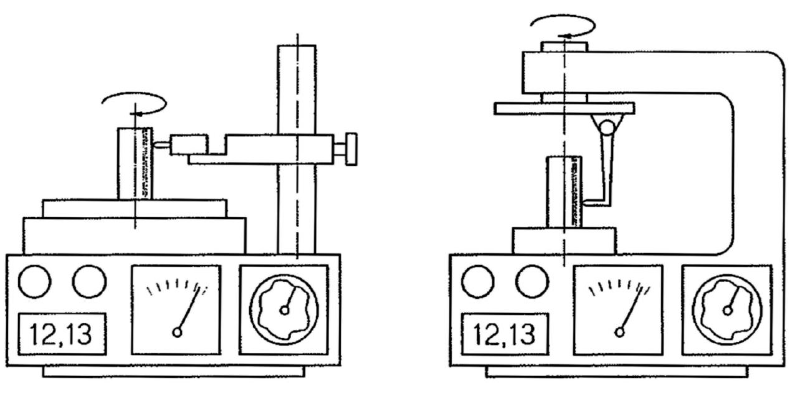
Slika 7: Merilnik z vrtečim merjencem in tipalom.
VALJNOST
Valjnost uporabljamo, kadar mora imeti sestavni del tako dobro krožnost, kot tudi ravnost, kot npr. odmična gred ali pozicionirni čepi. Krožnost se nanaša le na pravokotni presek, valjnost pa na kompletno površino. Valjnost najpreprosteje merimo na napravi, vidni na sliki 8 (nameščena urica na nosilcu, kos na rotirajoči se mizi).
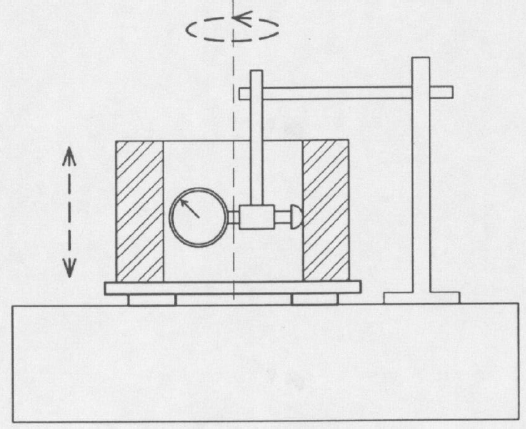
Slika 8: Naprava za merjenje valjnosti.
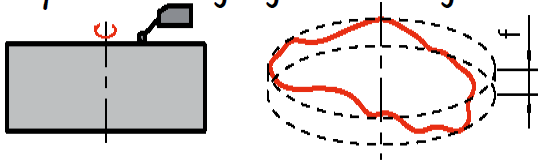
Na sliki 9 je prikazana modra krivulja, ki je izmerjeni profil na mestu, ki ga na merjencu simbolično označuje rdeča črta.
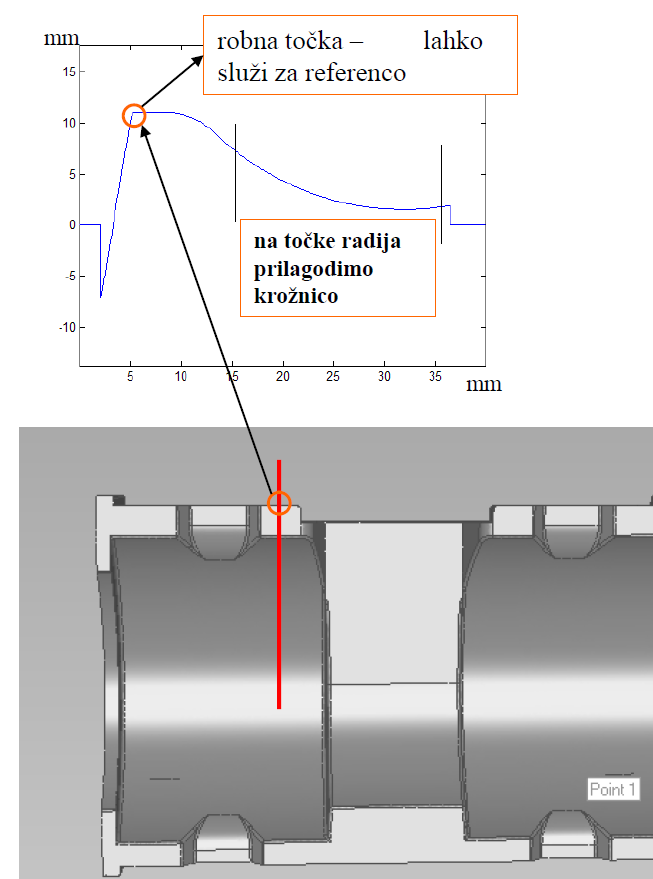
Slika 9: Primer merjenja in rezultirajoči graf.
Na sliki 10 pa je prikaza nstroj, ki lahko meri ravnost, krožnost kakor tudi cilindričnost (Mahr MMQ 400).

Slika 11: Primer stroja, ki lahko meri tri različne tolerance oblike.
Za zelo natančna merjenja okroglosti, koncentričnosti, soosnosti, pravokotnosti čelnih ploskev proti plašču valja in vzporednosti čelnih ploskev obstajajo posebni merilniki okroglosti. Najboljše izvedbe so tako občutljive, da je na njih mogoče meriti tudi hrapavost otipavanih ploskev. Nepravilnosti običajno prikažejo v obliki krožnega diagrama (slika 12). Odstopke okroglosti lahko povečajo od 20 do 20000 krat.
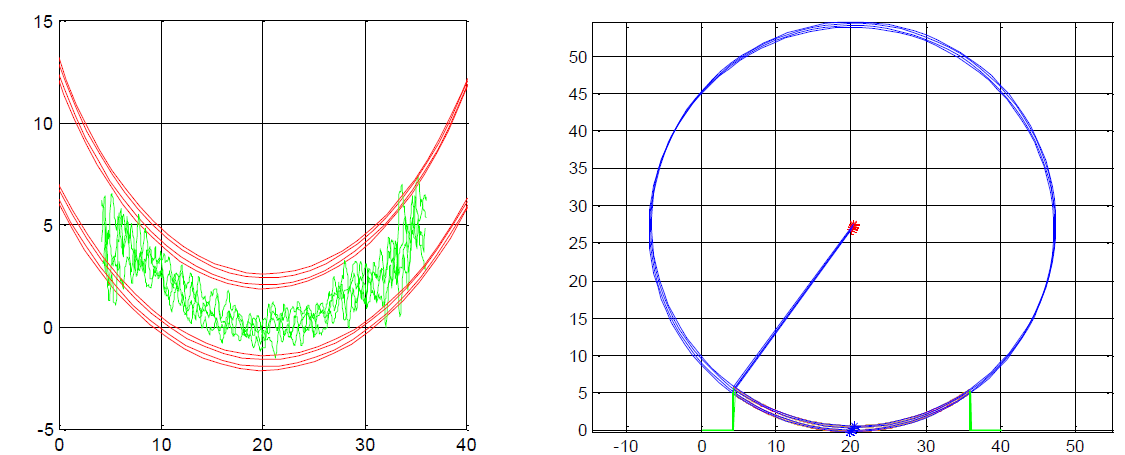
Slika 12: Primer krožnih diagramov.
OBLIKA ČRTE
S zgoraj omenjenimi stroji, predvsem pa CMM stroji, lahko merimo tudi obliko črte ali profila. To je kompleksna toleranca, ki definira uniformno mejo okoli površine, znotraj katere morajo ležati elementi površine. Ta toleranca hkrati nadzira obliko, velikost, orientacijo ter včasih tudi lokacijo posameznega gradnika. Profil je 3D toleranca, ki velja v vse koordinatne smeri, ne glede na risarski pogled, v katerem je bila definirana. Ta toleranca se navadno uporablja za kose z kompleksnimi zunanjimi oblikami ter konstantimi prerezi. Primer takšne tolerance je prikazan na sliki 13.
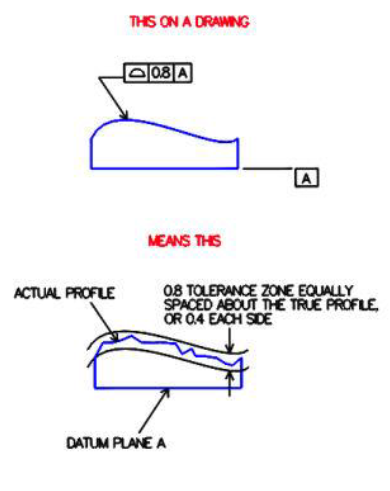
Slika 13: Primer pomena tolerance oblike črte ali profila.
MERITVE IN PREVERJANJE NAVOJEV
Osnovne veličine navojev, ki jih moramo meriti ali preverjati so:
-zunanji (veliki) premer
-srednji premer (premer navoja)
-notranji (mali) premer
-korak navoja
-profila navoja (zajema kot med bokoma zaokrožitev ali prirez na vrhu in zaokrožitev v dnu navoja)
Zunanji premer na vijakih merimo s kljunastim ali vijačnim merilom (izjemoma natančneje). Pri množinski izdelavi ga pogosto primerjamo tolerančno z navadnimi objemnimi merili.
Srednji premer navoja na vijakih merimo z merilnimi iglicami, ki imajo za vssako velikost navoja standardiziran premer, izbran tako, da se bokov navoja po možnosti dotikajo na srednjem premeru.
Notranji premer na vijakih merimi z merilnimi nožički, pri čemer od dobljene mere prek nožičkov odštevamo dve višini nožička. Mero prek iglic ali nožičkov izmerimo s kljunastim ali vijačnim merilom, veliko lažje pa na posebnem merilniku premerov navoja, ki ima vdelano vijačno merilo.
Korak navoja merimo s posebnimi komparatorji, ki imajo dve tipali, na koncu izoblikovani v kroglico. Največkrat pa ga merimo z merilnim mikroskopom, za hitro, približno preverjanje uporabljamo šablone v obliki standardnega profila navoja.
Na sliki 14 so grafično prikazana merilne veličine navojev.
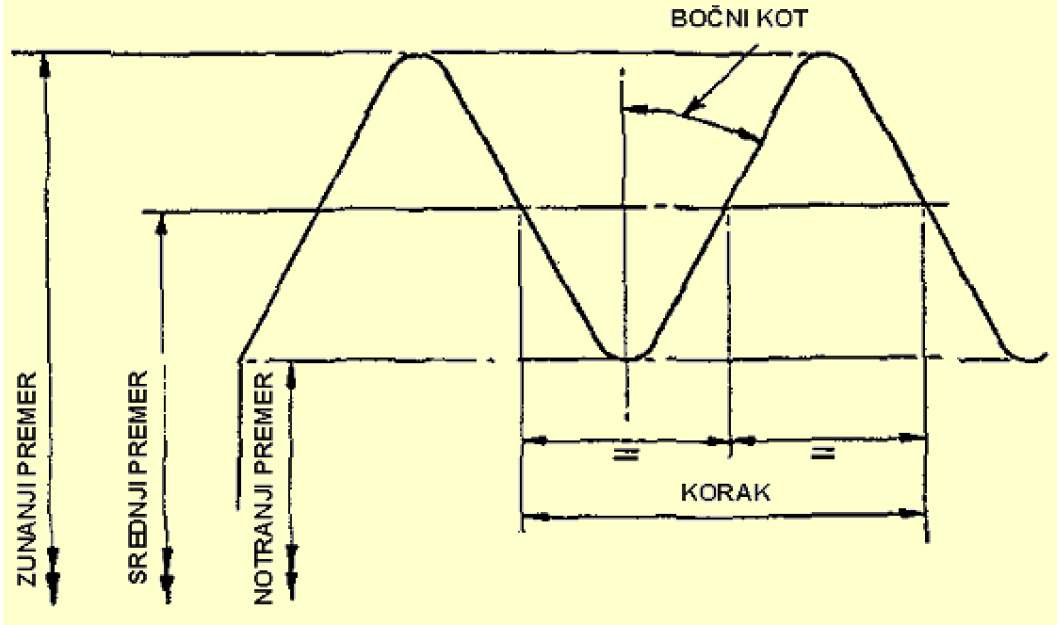
Slika 14: Grafični prikaz merilnih veličin za navoje.
ODSTOPKI NAVOJEV
- Navoj se skoraj vedno uporablja v vijačnih zvezah.
- Sila se prenaša iz vijaka na matico ali obratno.
- Odstopki pri navojih morajo zadostiti sledečim pogojem:
- Omogočanje zamenjave matice ali vijaka
- Prenašati zahtevano silo
- V vrhovih navojev mora biti minimalna zračnost
Grafični prikaz odstopkov navojev je prikazan na sliki 15.
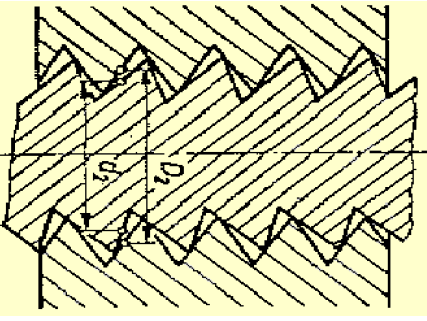
Slika 15: Grafični prikaz odstopka navojev.
KONTROLA NAVOJEV
V praksi se navoj ponavadi ne meri ampak samo kontrolira. Uporabljamo mejne kalibre (‘gre’, ‘ne gre’). Ne kontroliramo vsake veličine posebej, ampak hkrati več veličin, ki so med seboj odvisne. Obstaja nevarnost, da navoj napačno ocenimo, zato moramo navoj tudi meriti.
Spodnja tabela (tabela 1) prikazuje pregled metod merjenja navojev.
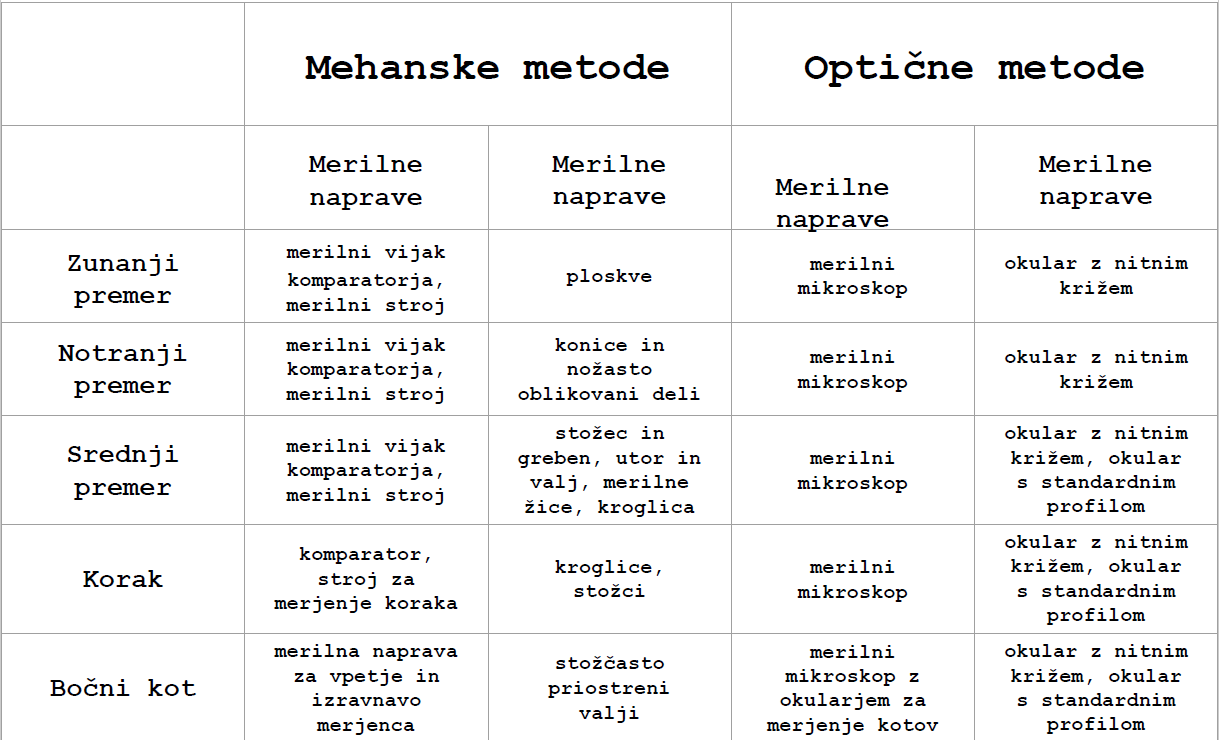
Tabela 1: Pregled merilnih metod navojev.
MEHANSKE METODE – MERJENJE ZUNANJEGA PREMERA
- primerna skoraj vsa merila za merjenje okroglih premerov
- merilni element – merilne ravne ploskve
- premer merilnih ploskev večji od koraka navoja, sicer zdrsne v utor (merilna kladica)
- merilna sila ne sme biti prevelika (sploščitev temena navoja – majhni premeri)
MEHANSKE METODE – MERJENJE NOTRANJEGA PREMERA
- merilna orodja enaka kot pri merjenju zunanjega premera
- uporabljamo posebne merilne elemente, kot so merilne konice in merilne vilice
Primer merjenja z dvema konicama je prikazan na sliki 16. Konici vstavimo tako, da se dotikata dna utora. Dotikališči nista nasproti – premaknjeni sta za polovico koraka (d1 majši od M, glej sliko 16). Notranji premer se izračuna po enačb, vidni na sliki 17.
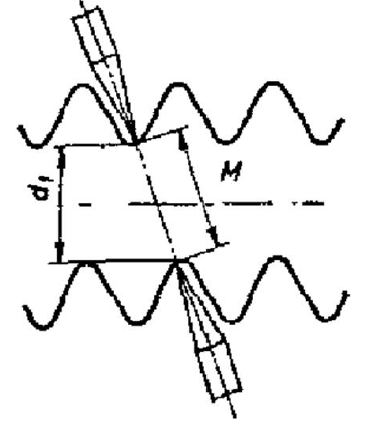
Slika 16: Primer merjenja med dvema konicama.
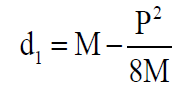
Slika 17: Enačba za izračun premera.
Lastnosti merjenja z dvema konicama:
- izognemo se preračunavanju
- merilni telesi sta vrtljivi
- natančnost meritve je odvisna od odstopanja koraka
- če korak ni razdalja med konicama ne merimo v najnižji točki navoja
- uporaba dveh prizmatičnih vložkov (merjenec vpet med konice)
Na slikah 18-23 so vidne stroji in naprave za merjenje navojev.
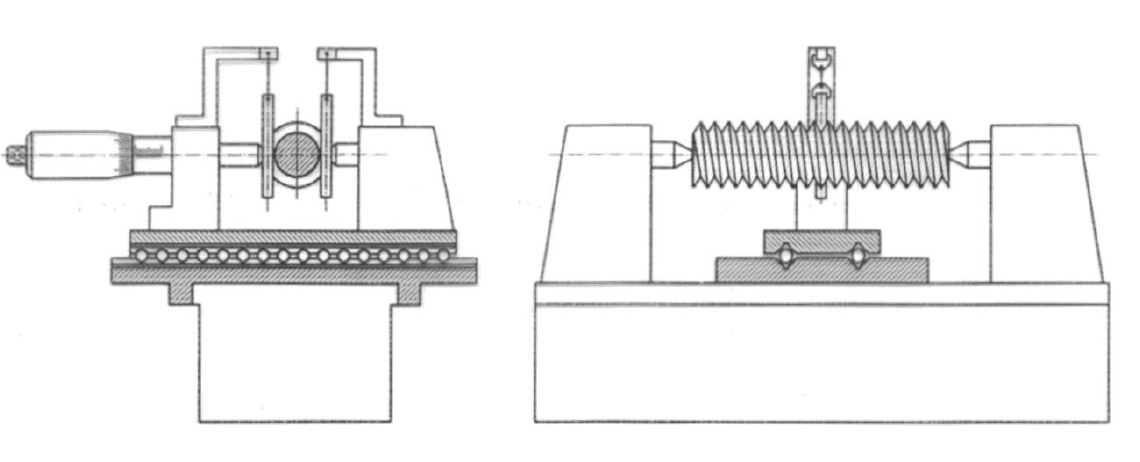
Slika 18: Merilnik premerov navoja z vdelanim vijačnim merilom.
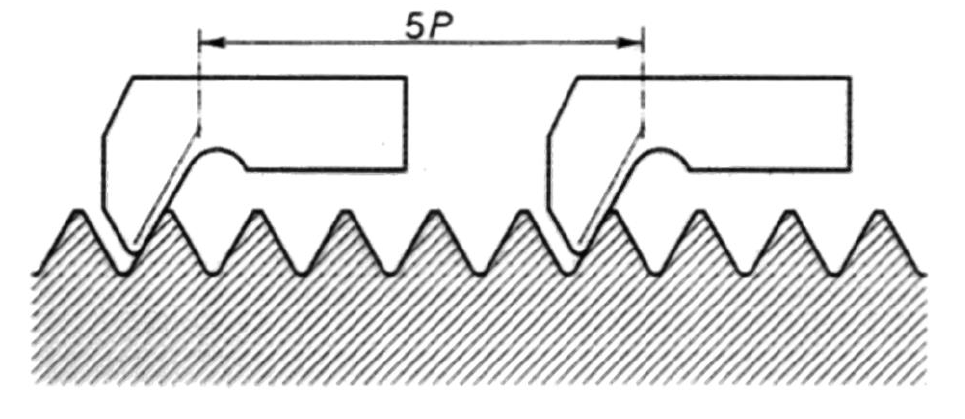
Slika 19: Nožički za merjenje koraka z merilnim mikroskopom.
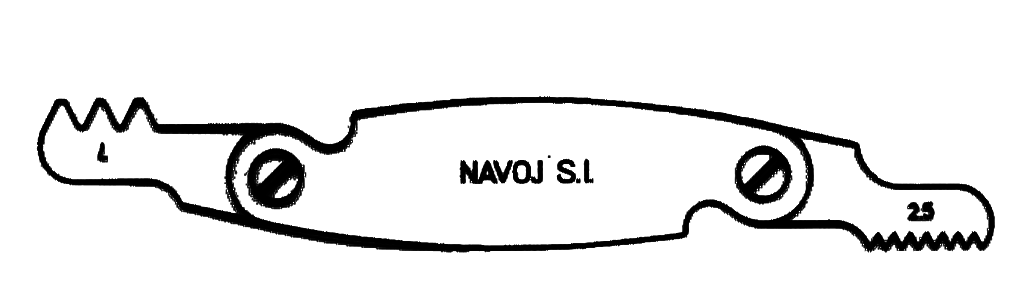
Slika 20: Šablone za preverjanje koraka in profila navoja.
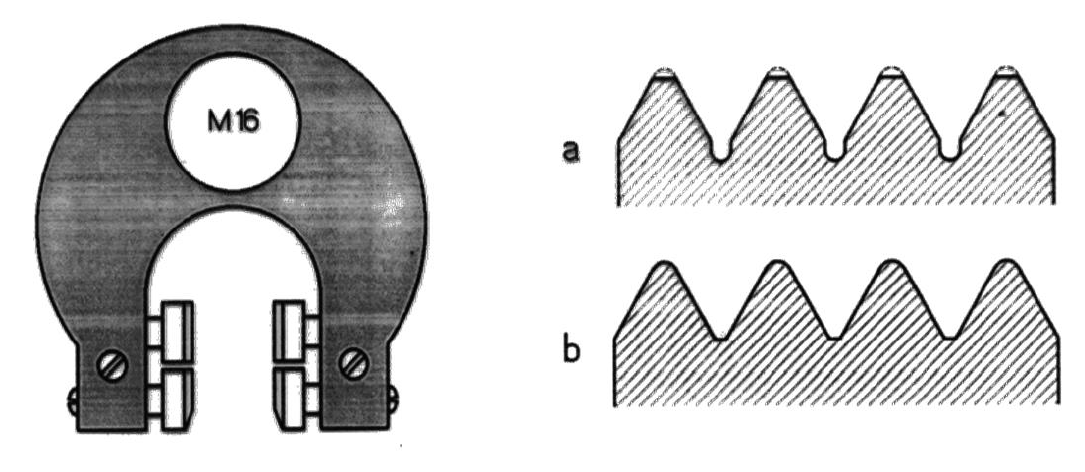
Slika 21: a. profil tipal za merjenje srednjega premera b. profil tipal za preverjanje celotnega profila.
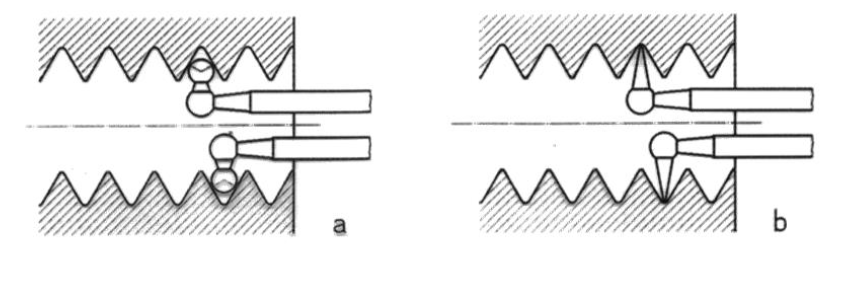
Slika 22: Merjenje s tipali pri notranjem navoju: a.merjenje srednjega premera, b. merjenje zunanjega premera.
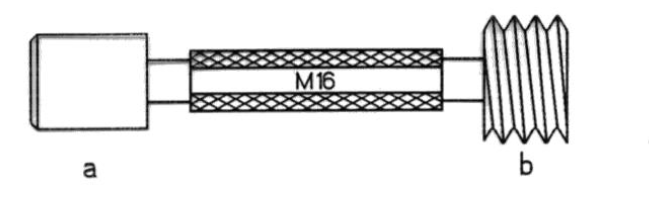
Slika 23: Merilni čep za tolerančno preverjanje notranjih navojev: a. stran za preverjanje notranjega premera, b. stran za preverjanje celotnega navoja.